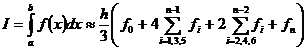METODE SIMPSON 1/8 DAN 3/8 BESERTA CONTOH PROGRAM

BAB I

PENDAHULUAN

A.    Latar Belakang

Seiring pesatnya perkembangan teknologi dan kemajuan zaman, maka diperlukan suatu produk dengan ketelitian dan akurasi yang tinggi dan waktu pengerjaan yang singkat. Adanya perkembangan teknologi informasi yang sangat pesat pada saat ini mendorong para praktisi untuk mengembangkan cara baru agar pekerjaan analisa dapat dilakukan dengan lebih baik dan lebih efektif. Sudah banyak persoalan di bidang teknik maupun sains yang dapat diselesaikan dengan menggunakan permodelan matematika. Sering kali permodelan matematika tersebut muncul dalam bentuk yang tidak ideal, sehingga tidak dapat diselesaikan dengan menggunakan metode analitik untuk mendapatkan solusi sejati (exact solution).

Jika persoalan-persoalan yang kita hadapi tidak dapat diselesaikan dengan metode permodelan matematika metode analitik menggunakan dalil-dalil kalkulus, maka solusinya dapat diperoleh dengan metode numerik. Metode numerik secara harfiah berarti suatu cara berhitung dengan menggunakan angka-angka, sedangkan secara istilah metode numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematik sehingga dapat diselesaikan dengan operasi aritmatika biasa.

Dengan menggunakan metode numerik, solusi exact dari persoalan yang dihadapi tidak akan diperoleh. Metode numerik hanya bisa memberikan solusi yang mendekati atau menghampiri solusi sejati sehingga solusi numerik dinamakan juga solusi hampiran (approximation solution). Pendekatan solusi ini tentu saja tidak tepat sama dengan solusi sejati, sehingga ada selisih antara keduanya. Solusi tersebut disebut solusi galat (error). Semakin kecil galat yang diperoleh berarti semakin dekat solusi hampiran yang diperoleh dengan solusi sejatinya.

BAB II

PEMBAHASAN

A.    Kaidah Simpson 1/3

Kaidah simpson 1/3 adalah kaidah yang mencocokkan polinomial derajat 2 pada tiga titik data diskrit yang mempunyai jarak yang sama. Hampiran nilai integrasi yang lebih baik dapat ditingkatkan dengan menggunakan polinom interpolasi berderajat yang lebih tinggi. Misalkan fungsi f(x) dihampiri dengan polinom interpolasi derajat 2 yang grafiknya berbentuk parabola. Luas daerah dihitung sebagai hampiran nilai integrasi adalah daerah di bawah parabola (Gambar 3.1). untuk itu, dibutuhkan 3 buah titik data, misalkan (0,f(0)),(h,f(h)),  dan (2h,f(2h)).

Gambar 3.1 Kaidah Simpson 1/3

Namun penggunaan kaidah Simpson 1/3 mensyaratkan jumlah upselang (n) harus genap, ini berbeda dengan kaidah trapesium yang tidak memiliki persyaratan mengenai jumlah selang.

Algoritma Metode Integrasi Simpson 1/3:

1. Mendefinisikan fungsi yang akan diintegrasikan y=f(x).
2. Menentukan batas bawah (a) dan batas atas (b) integrasi
3. Menentukan jumlah segmen atau pias n dengan syarat n genap
4. Menghitung lebar segmen yaitu h=(b-a)/n .
5. Menentukan nilai integrasi menggunakan kaidah Simpson 1/3
   

6.                6.Menentukan nilai integrasi sejatinya

CONTOH PROGRAM MENGGUNAKAN MATLAB

SOURCE CODE PROGRAM

 Clc;

f=(@(x)3^(x.^2)+3.*x;

a=input(‘input batas bawah= ‘);

b=input(‘input batas atas = ‘);

k=input(‘input partisi : ‘);

If a>b

                c=b;

                b=a;

                a=c;

End

deltax = (b-a)/k;

i=1;

z=0;

y=0;

while i<=k-1

                z=z+f(a+(i*deltax));

                i=i+z;

end

i=2;

while i<=k-2

y=y+f(a+(i*deltax));

i=i+2;

end

luas daerah=(deltax/3)*(f(a)+(4*z)+(2*y)+f(b))

fplot(f,[0,2])

OUTPUT PROGRAM

tinggal run Source code di atas dengan memasukaan batas bawah = 0 , batas atas =2 dan jumlah partisi =5, maka hasilnya akan didapat. khusus di  Metode simpson 1/8 ini jumlah partisi harus ganjil tidak boleh genap. karna kalau genap jumlah luasnya tetap entah berapapun nilai batas atas dan bawahnya. maka dari itu pada program saya menggunakan nilai partisinya ganjil yaitu 5.Dan setrusnya jika partisinya di berikan bilangan ganjil yang lebih besar lagi maka nilai luas daerahnya semakin besar

B.     Kaidah Simpson 3/8

Seperti halnya pada kaidah Simpson 1/3, hampiran nilai integrasi yang lebih teliti dapat ditingkatkan terus dengan mengunakan polinom interpolasi berderajat lebih tinggi pula. Misalkan sekarang fungsi f(x) kita hampiri dengan polinom interpolasi derajat 3. Luas daerah yang dihitung sebagai hampiran nilai integrasi adalah daerah di bawah kurva polinom derajat 3 tersebut parabola (Gambar). Untuk membentuk polinom interpolasi derajat 3, dibutuhkan 4 buah titik data, misalkan titik-titk tersebut (0, f(0)), (h, f(h)), (2h, f(2h)), dan (3h, f(3h)).

Gambar 3.2 Kaidah Simpson 3/8

Kaidah simpson 3/8 memiliki orde galat yang sama dengan orde galat kaidah simpson 1/3 namun dalam parktek, kaidah simpson 1/3 lebih disukai daripada kaidah simpson3/8, karena dengan tiga titik (simpson 1/3) sudah diperoleh orde ketelitian yang sama dengan 4 titik (simpson 3/8). Tetapi untuk n kelipatan tiga , kita hanya dapat menggunakan kaidah simpson 3/8, dan bukan simpson 1/3.

Algoritma Metode Integrasi Simpson 3/8:

1.       Mendefinisikan fungsi yang akan diintegrasikan y=f(x).
2.       Menentukan batas bawah a dan batas atas b integrasi
3.       Menentukan jumlah segmen atau pias n dengan syarat n kelipatan 3
4.       Menghitung lebar segmen yaitu h=(b-a)/n .
5.       Menentukan nilai integrasi menggunakan kaidah Simpson 3/8                                                                                       
6.      Menentukan nilai integrasi sejatinya

CONTOH PROGRAM  MENGUNAKAN MATLAB

SOURCE CODE PROGRAM

Clc;

f=(@(x)3^(x.^2)+3.*x;

a=input(‘input batas bawah= ‘);

b=input(‘input batas atas = ‘);

k=input(‘input partisi : ‘);

If a>b

                c=b;

                b=a;

                a=c;

End

deltax = (b-a)/k;

i=1;

z=0;

y=0;

while i<=k-1

                z=z+f(a+(i*deltax));

                i=i+z;

end

i=2;

while i<=k-2

y=y+f(a+(i*deltax));

i=i+2;

end

luas daerah=3*(deltax/8)*(f(a)+(3*z)+(2*y)+f(b))

fplot(f,[0,2])

OUTPUT PROGRAM

Penjelasan

     Untuk mencari luas daerah dengan menggunakan metode simpson 3/8.
kita harus menginput batas bawah , atas dan menentukan jumlah partisinya. Setelah itu jika batas bawah lebih besar dari batas atas, maka nilai c=b, b=a, dan a=c. Kemudian dicarilah deltax = (b-a)/k. Dengan i=1, g&h=0.Lalu untuk mencari  luas daerah nya di gunakan luasdaerah=3*(deltax/8)*(f(a)+(3*z)+(2*y)+f(b)). Setelah itu akan muncul hasil dari luas daerahnya .

 

 

 

 

 

 

 

 

BAB III

KESIMPULAN

Pada metode Simpson Menggunakan Parabola,seperti pada metode trapezoida yg menggunakan trapesium. dalam metode ini makin banyak jumlah partisi yang kita gunakan maka akan mendekati nilai luas yang sebenarnya.Jadi Kalau metode Simpson 1/8 memiliki kekurangan dan metode simpson 3/8 memiliki hampiran nilai integrasi yang lebih teliti danmengunakan polinom interpolasi berderajat lebih tinggi pula.

Sekian Penjelasan Dari saya.. Terimah Kasih Telah berkunjung ☺ Jangan lupa Share blog ini agar dapat berkembang .

INTEGRASI RIEMANN

INTEGRASI RIEMANN

BAB I Pendahuluan

     A.Latar Belakang

      Konsep integral sering digunakan untuk menentukan luas daerah di bawah kurva. Selain itu, integral juga sering digunakan untuk mencari penyelesaian dari suatu model matematika. Seiring dengan perkembangan zaman, saat ini banyak ditemui software-software yang sudah menyertakan operasi integral sehingga memudahkan pengguna dalam mencari nilai integral suatu fungsi. Adapun semua itu tidak terlepas dari awal mula ilmu kalkulus yang telah mengalami perkembangan dan juga perbaikan. pada tahun 1850-an, Bernard Riemann berhasil menemukan bentuk integral yang baru dan berbeda. Riemann memisahkan konsep integrasi dari diferensiasi dan menggunakan ide penjumlahan dan proses limit untuk menentukan luas daerah di bawah kurva. Selanjutnya bentuk integral ini disebut integral Riemann. Setiap fungsi kontinu f pada [a b, ] dijamin juga terintegral Riemann pada [a ,b] .

BAB II Pembahasan

     A.Pengertian Integrasi Riemann

             

      Metode integral Reimann didefinisikan dengan:

Pada metode ini, luasan yang dibatasi oleh y = f(x) dan sumbu x dibagi menjadi n bagian pada rangeyang akan dihitung. Kemudian dihitung tinggi dari setiap step ke-I yaitu  f(x_i). L_i adalah luas setiap persegi panjang dimana L_i=f(x_i) ∆x_{i .}Pada metode ini, luasan yang dibatasi oleh y = f(x) dan sumbu x dibagi menjadi n bagian pada range X=[a,b] yang akan dihitung. Kemudian dihitung tinggi dari setiap step ke-I yaitu f(x_i). L_i adalah luas setiap persegi panjang dimana L_i=f(x_i) ∆x_i  .

Gambar

 pembagian kurva menjadi sejumlah segiempat

Luas keseluruhan adalah jumlah Li dan dituliskan :

L = L₀ + L₁ + L₂ + ... + L_n

                          = f(X₀) ∆X₀ + f(X₁) ∆X₁ + f(­X₂) ∆X₂ + ... + f(X_n) ∆X_n

                = 

Bila diambil ∆X₀ = ∆X₁ = ∆X₂ = ...=  ∆X_n = L maka didapat metode integral Riemann sebagai berikut :

Algoritma Metode Integral Reimann

1.   Definisikan fungsi f(x)

2.   Tentukan batas bawah dan batas atas integrasi

3.   Tentukan jumlah pembagi area N

4.   Hitung h=(b-a)/N

5.   Hitung  

     B. Contoh Program dan Output

SOURCE CODE

OUTPUT PROGRAM

GAMBAR GRAFIK

C. Penjelasan Program

         Diberikan sebuah fungsi f(x) = x^2+2*x+3.Akan dicari nilai luas daerah dari fungsi tersebut dengan menggunakan matlab.dengan mengikuti proses algoritmanya maka masukkan nilai batas bawah = 1 dan batas atas = 2 serta jumlah pembagi areanya=12. Maka hasil luas dri fungsi tersebut adalah 8,5428241.

BAB III Kesimpulan

     A.Kesimpulan

Integrasi Reimann merupakan salah satu metode yang digunakan untuk menyelesaikan integrasi numerik. metode Integrasi Reimann yang lebih mudah dipergunakan karena rumusnya lebih sederhana dan mudah untuk di pahami.

Terimakasih Sudah Berkunjung dan Membaca artikel saya. Semoga Membantu Dan Bermanfaat ... Jangan Lupa untuk share artikel ini agar bisa bermanfaat bagi yang lain juga.

Penerapan Analisis Linear Berganda Di kehidupan Sehari-hari

PENERAPAN ANALISIS LINEAR BERGANDA

AnggotaKelompok        :    1. Uli Adelina Siahaan                  (170803039)

  2. Elsadday Easter Arga                 (170803051)

  3. Hamonangan Simatupang          (170803059)

  4. Thresya Hotprita Siregar           (170803097)

  5. Bedran Simbolon                         (170803117)

Mata Kuliah                            : Analisis Regresi Linear

Dosen                                      : Dra. Laurentina Pangaribuan, M.S

S1 MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

UNIVERSITAS SUMATERA UTARA

MEDAN

2019

A.  Analisis Regresi Berganda

Analisis regresi linear berganda adalah pengembangan dari analisis regresi linear sederhana dimana terdapat lebih dari satu variabel independen X. Analisis ini digunakan untuk melihat sejumlah variabel independen X₁ , X₂ , … X_k terhadap variabel dependen Y berdasarkan nilai variabel-variabel independen X₁ , X₂ , … X_k.

Perbedaaan antara regresi sederhana dengan regresi berganda terletak pada jumlah variabel bebasnya. Jika dalam regresi sederhana jumlah variabel bebas yang digunakan untuk memprediksi variabel tergantung hanya satu, maka regresi berganda jumlah variabel bebas yang digunakan untuk memprediksi variabel tergantung lebih dari satu. Dalam regresi berganda seluruh variabel bebas dimasukkan kedalam perhitungan regresi serentak.

Dengan demikian dipeorleh persamaan regresi guna memprediksi variabel terikat dengan memasukkan secara serentak serangkaian variabel bebas. Dalam persamaan regresi dihasilkan konstanta dan koefisien regresi bagi masing-masing variabel bebas.

B.   Model Regresi Berganda

Regresi berganda digunakan unuk menganalisis hubungan kausal beberapa variabel bebas (X) terhadap satu variabel tergantung (Ŷ). Model yang digunakan untuk analisis regresi berganda sebagai berikut:

Ŷ = a + b₁X₁ + b₂X₂ + …. + bnXn + ε

·         Ŷ = nilai yang diramalkan (diprediksi)

·         a  = konstanta/intercep

·         b₁  = koefisien regresi/slope untuk X₁

·         X₁ = variabel bebas X₁

·         b₂  = koefisien regresi/slope untuk X₂

·         X₂ = variabel bebas X₂

·         bn  = koefisien regresi/slope untuk Xn

·         Xn = variabel bebas Xn

·         ε  = nilai residu

C.   Langkah-Langkah Komputasi

   1.   Entri data pada tabel kedalam Data View dan Variable View format SPSS data viewer sebagai berikut:

2.     Analyze | Regression | Linier

Pindahkan variabel X ke kolom Independent(s) dan variabel Y ke kolom Dependent

3.    KlikOK, maka akan muncul hasil nya: 

D.  Hasil

Populasi :MahasiswaAktifMatematikaAngkatan 2017

Sampel : 10 orang (10% dari 98 orang)

Data :

Keterangan Variabel :

Hasil menggunakan SPSS :

a.       Analisis Tabel Model Summary

·         R

Menunjukkan korelasi antara variable bebas dengan variable tergantungnya (tidak bebas).Dalam hal ini dikarenakan regresi linier berganda maka dikatakan bahwa korelasi berganda antara variabel X₁ dan X₂ terhadap variabel Y adalah sebesar 0,926.

·         R Square

Koefisien determinasi yang menunjukkan pengaruh langsung variabel X₁ dan X₂ terhadap variabel Y yang dinyatakan dalam persentase.Koefisien determinasi 0,858 berarti bahwa variabel X₁ dan X₂ memengaruhi secara langsung variabel Y sebesar 85,8% sedangkan (100-85,8)%= 14,2% dipengaruhi oleh faktor lain diluar variabel X₁ dan X₂.

·         Adjusted R Square

Adjusted R Square merupakan koefisien determinasi yang telah terkoreksi dengan jumlah variable dan ukuran sampel sehingga dapat mengurangi unsur bias jika terjadi penambahan variabel. Adjusted R Square sebesar 0,817 berarti variasi variabel Y dapat dijelaskan oleh variabel X₁ dan X₂ sebesar 81,7% atau variabel X₁ dan X₂  memengaruhi variabel Y sebesar 81,7%.

·         Error of the Estimate

Std. Error of the Estimate menunjukkan penyimpangan antara persamaan regresi dengan nilai dependent  riil sebesar 84,716 satuan variabel dependent (jika variabel Y dalam satuan maka besarnya penyimpangan adalah sebesar 84,716 satuan).Semakin kecil nilai Std. Error of the Estimate maka semakin baik persamaan regresi tersebut sebagai alat prediksi.Pada umumnya S.E < Std. Deviasi ada  pula yang menyatakan S.E < 4,00

b.      Analisis Tabel ANOVA

·         Sum of Square Regression

Sum of Square Regression (SSReg) merupakan nilai yang menunjukkan jumlah kuadrat dari selisih antara nilai prediksi dengan nilai rata-rata prediksi sebesar 302808,536.

·         Sum of Square Residual

Sum of Square Residual (SSRes) merupakan nilai yang menunjukkan jumlah kuadrat dari selisih antara nilai riil prediksi sebesar 50237,864.

·         Sum of Square Total

Sum of Square Total (SSSum) merupakan nilai yang menunjukkan jumlah kuadrat dari selisih antara nilai riil dengan nilai rata-rata Y riil sebesar 353046,400.

·         df Regression

df Regression dirumuskan dengan  k-1 dimana k adalah jumlah variabel. Dimana k =2 makadf= 3-1=2.

·         df Residual

df Residual dirumuskan n-k dengan n jumlah sampel (responden) dan k jumlah variabel. n = 10 dan k = 3, makadf = 10 – 3 = 7.

·         df Total

df Total dirumuskan n -1 dengan n jumlahsampel (responden). Dimana n = 10, maka df = 10 -1 = 9.

·         Mean Square Regression

Mean Square Regression (MSReg) diperoleh dari perbandingan antara Sum of Square Regression dengan df Regression sebesar 151404,268.

·         Mean Square Residual

Mean Square Residual (MSRes) diperoleh dari perbandingan antara Sum of Square Residual dengan df Residual sebesar 7176,838.

·         F hitung

F hitung diperoleh dari perbandingan antara Mean Square Regression dengan Mean Square Residual sebesar 21,096.

·         Sig.

Sig. merupakan nilai yang menunjukan titik kesalahan yang terjadi jika nilai F-hitung sebesar 21,096.Ternyata tingkat kesalahan atau probabilitas sebesar 0,001 yang berarti lebih kecil dari 0,05. Jadi dapat disimpulkan bahwa variable bebas secara simultan mampu menjelaskan perubahan pada variable tergantung, atau model dinyatakan cocok atau fit.

c.       Analisis Tabel Coefficients

·         Unstandardize Coefficients (Constant)

Unstandardize Coefficients (Constant) merupakan konstanta regresi yang dinotasikan dengan a, yang mengandung pengertian bila tidak ada perubahan pada variabel X (X =0) maka variabel tidak memiliki penambahan nilai dimana nilainya Constant, yaitu a = -415,014

·         Unstandardize Coefficients Variabel X₁

Unstandardize Coefficients variabel X merupakan koefisien arah regresi b, yang berarti jika variabel X₁ mengalami peningkatan 1 satuan, maka variabel Y akan meningkat sebesar 78,027.

·         Unstandardize Coefficients Variabel X₂

Unstandardize Coefficients variabel X merupakan koefisien arah regresi b, yang berarti jika variabel X₂ mengalami peningkatan 1 satuan, maka variabel Y akan meningkat sebesar 144,308.

·         Standard Error (Constant)

Standard Error (Constant) merupakan penyimpangan dari konstanta yang ada dalam model persamaan regresi sebesar 168,399.

·         Error Variabel X₁

Std. Error Variabel X₁ menunjukkan penyimpangan koefisien regresi variabel X₁. Semakin kecil penyimpangan dalam koefisien regresi itu berarti semakin berarti kontribusi variabel X₁ tersebut terhadap variabel Y sebesar 19,945.

·         Error Variabel  X₂

Std. Error Variabel X₂ menunjukkan penyimpangan koefisien regresi variabel X₂ Semakin kecil penyimpangan dalam koefisien regresi itu berarti semakin berarti kontribusi variabel X₂ tersebut terhadap variabel Y sebesar 40,696.

·         Standardized Coefficients (Beta) Variabel X₁

Standardized Coefficients (Beta) variabel  X₁ merupakan koefisien jalur atau koefisien regresi tetapi semua variable telah ditransformasi terlebih dahulu ke dalam bentuk standardized sebesar 0,593.

         Standardized Coefficients (Beta) Variabel X₂

Standardized Coefficients (Beta) variabel X₂ merupakan koefisien jalur atau koefisien regresi tetapi semua variable telah ditransformasi terlebih dahulu ke dalam bentuk standardized sebesar 0,538.

·         t-Constant

t-Constant digunakan untuk mengetahui apakah signifikasi intercept (konstantaregresi) namun nilai intercept biasanya tidak diuji. Yang di uji adalah nilai t-stat koefisien regresinya.

·         t-variable X₁

t-variable X₁ merupakan perbandingan antara Unstandardize Coefficients variabel X₁ dengan Std. Error Variabel X₁, digunakan untuk mengetahui signifikasi variabel X₁. Jika nilai lebih besar dari nilai t-tabel dengan df:α, (n-k-1) maka variable tersebut memiliki pengaruh yang signifikan terhadap variable tergantung.Dengan df: α, (n-k-1) atau 0,001 (10-2) diperoleh nilai t-tabel sebesar 2,365. Karena nilai thitung 3,912 >ttabel (2,365), maka dapat disimpulkan bahwa variabel X₁ memiliki pengaruh positif terhadap variabel Y.

·         t-variable X₂

t-variable X₂ merupakan perbandingan antara Unstandardize Coefficients variabel X₂ dengan Std. Error Variabel X₂, digunakan untuk mengetahui signifikasi variabel X₂. Jika nilai lebih besar dari nilai t-tabel dengan df:α, (n-k-1) maka variable tersebut memiliki pengaruh yang signifikan terhadap variable tergantung. Dengan df: α, (n-k-1) atau 0,05 (10-3) diperoleh nilai t-tabel sebesar . Karena nilai thitung 3,546 >ttabel (2,365), maka dapat disimpulkan bahwa variabel X₂ memiliki pengaruh positif terhadap variabel Y.

·         Variable X₁

Sig. Variable X₁ merupakan angka yang menunjukkan besarnya tingkat kesalahan pada nilai thitung X₁ yang diperoleh 3,912.Jika nilai t-variabel X semakin besar maka nilai kesalahan Sig. akan semakin kecil. Karena nilai Sig. variabel X₁ (0,006) (< 0,05) dengan arah koefisien positif, maka dapat disimpulkan bahwa variabel X₁ berpengaruh positif signifikan terhadap variabel Y.

·         Variable X₂

Sig.Variable X₂merupakan angka yang menunjukkan besarnya tingkat kesalahan  pada nilai thitung X₂ yang diperoleh 3,546.Jika nilai t-variabel X semakin besar maka nilai kesalahan Sig. akansemakin kecil. Karena nilai Sig. variabel X₂ (0,009) (< 0,05) dengan arah koefisien positif, maka dapat disimpulkan bahwa variabel X₂ berpengaruh positif signifikan terhadap variabel Y.

E.   Kesimpulan

Dari hasil di atas maka diperoleh :

1)      Persamaan regresi ganda : Ŷ = -415,014 + 78,027 X₁  +144,308X₂

2)      Hipotesis keberartian regresi parsial sebagai berikut:

·         Nilaithitung 3,912 >ttabel 2,365atau Sig. 0,006 (< 0,05) dengan demikian disimpulkan terdapat pengaruh positif yang signifikan X₁ terhadap Y.

·         Nilai  thitung 3,546>ttabel 2,365atau Sig. 0,009 (< 0,05) dengan demikian disimpulkan terdapat pengaruh positif yang signifikan X₂ terhadap Y.